<問題>
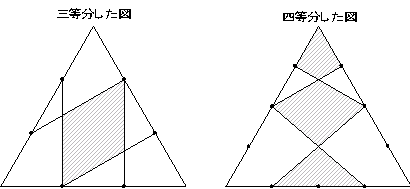
下図は、正三角形の各辺をそれぞれ三等分、四等分した図です。
(1) 各辺を三等分した図では、色のついた部分の面積は、正三角形の面積の【 】倍です。
(2) 各辺を四等分した図では、色のついた部分の面積は、正三角形の面積の【 】倍です。

(03年芝1回)
入試問題に挑戦第84回解答編
<解答>
いろいろなやり方がありますが、ここでは相似比を利用してみましょう。
(1) 図を回転して、三等分点を平行に結んで正三角形を3つに分割すると、斜線部はアとイに分けられ、この2つの面積は等しくなります。
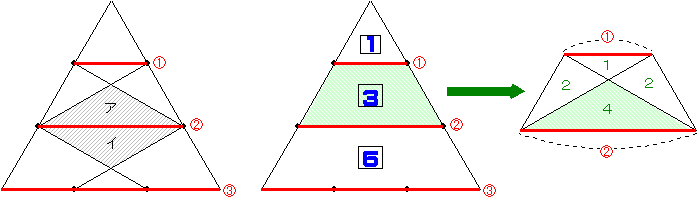
正三角形を3つに分割したときの面積比は、1:3:5となり、このうちアを含む台形をさらに対角線で4つに分けると面積比は1:2:2:4となります。
よって、正三角形の面積に対するアの面積の割合は、
![]()
となるので、求める斜線部の面積は、
![]()
(2) 上と同様に正三角形を4つに分割すると、斜線部はウ、エ、オ、カ、キに分けられ、カとキの面積は等しくなります。
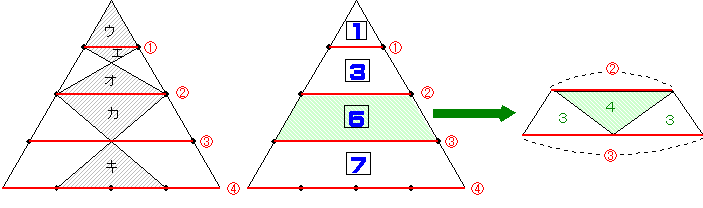
正三角形を4つに分割したときの面積比は、1:3:5:7となり、このうちエとオを含む台形は(1)と同様になり、カを含む台形は、さらに3つに分割して3:4:3となります。
これをもとに正三角形に対するそれぞれの割合を計算すると、
ウ … ![]()
エとオ … ![]()
カとキ … ![]()
以上から、求める斜線部の面積は、
![]()