
<問題>
下の図の円の半径は5cm、四角形の頂点はずべて円周の12等分する点である。この四角形の面積は【 】平方cmである。(02年灘)

入試問題に挑戦第61回解答編
<解答>
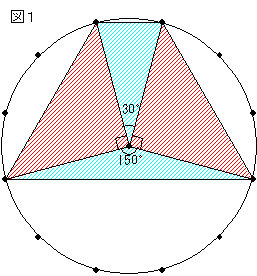
まず、図1のように円の中心から四角形の各頂点に直線を引いて、4つの三角形に分割します。このうち左右の赤い三角形は直角二等辺三角形なのですぐに面積は求めることができます。
5×5÷2=12.5(平方cm) … 左右の赤い三角形1個の面積
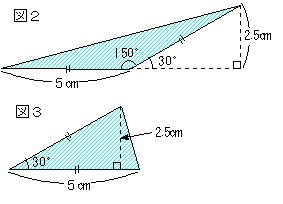
次に、上下の青い二等辺三角形については、図2、図3の通りいずれも底辺5cm、高さ2.5cmの三角形として面積を求めることができます。
5×2.5÷2=6.25(平方cm) … 上下の青い三角形1個の面積
以上から、 12.5×2+6.25×2=37.5(平方cm)