亙栤戣亜
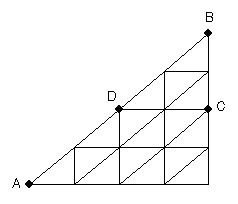
恾偺傛偆側摴傪丄俙抧揰偐傜俛抧揰傑偱屻傕偳傝偣偢偵峴偒傑偡丅

乮侾乯丂俙抧揰偐傜昁偢俠抧揰傪捠偭偰俛抧揰傊峴偔偵偼壗捠傝偺峴偒曽偑偁傝傑偡偐丅
乮俀乯丂俙抧揰偐傜俢抧揰傪捠傜偢偵俛抧揰傊峴偔偵偼壗捠傝偺峴偒曽偑偁傝傑偡偐丅
乮侽俀擭怷懞妛墍乯
丂
丂
丂
擖帋栤戣偵挧愴戞俆侾夞夝摎曇
亙夝摎亜
傛偔偁傞摴弴偺栤戣偱偡偑丄幬傔偺摴偑偁傞偺偱丄慻傒崌傢偣偱偼側偔丄壓偺恾偺條偵弴偵榓傪寁嶼偟偰偄偔偙偲偵偟傑偡丅
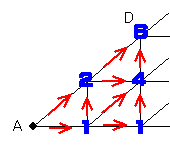
乮侾乯俠抧揰偐傜俛抧揰傑偱偺摴弴偼侾捠傝偟偐側偄偺偱丄俙抧揰偐傜俠抧揰傑偱偺摴弴傪悢偊傟偽傛偄偙偲偵側傝傑偡丅
丂丂弴偵榓傪寁嶼偟偰偄偔偲丄師偺條偵側傝傑偡丅
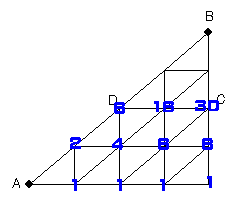
乮俀乯俢抧揰傪捠傜偢偵俛抧揰傊峴偔摴弴偺悢偊曽偼俀捠傝偁傝傑偡丅
丂丂嘆俛抧揰傊峴偔偡傋偰偺捠傝悢偐傜丄俢抧揰傪捠傞捠傝悢傪堷偔曽朄丅
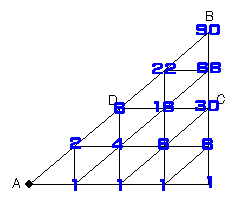
丂丂丂恾偺條偵丄俙抧揰偐傜俛抧揰傑偱峴偔摴弴偼俋侽捠傝偁傝傑偡丅偙偺偆偪丄俢抧揰傪捠傞摴弴偵偮偄偰偼丄
丂丂丂俙抧揰偐傜俢抧揰傑偱偑俇捠傝丄俢抧揰偐傜俛抧揰傑偱偑俇捠傝側偺偱丄俇亊俇亖俁俇捠傝丅
丂丂丂埲忋偐傜丄丂俋侽亅俁俇亖俆係乮捠傝乯
丂
丂丂嘇俢抧揰偵偮側偑傞摴傪巊傢偢偵摴弴偺榓傪寁嶼偡傞曽朄丅
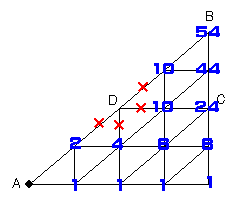
丂丂丂恾偺條偵丄俢抧揰偵偮側偑傞摴傪巊傢偢偵榓傪寁嶼偟偰丄俆係乮捠傝乯丅