<問題>
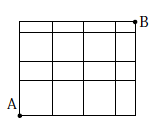
下の図のような道路があります。A地点からB地点まで最短の道のりで進むことにします。次の問いに答えなさい。

(1)曲がり角を3回曲がる方法は何通りありますか。
(2)曲がり角を4回曲がる方法は何通りありますか。
(04年頌栄女子学院)
入試問題に挑戦第134回解答編
<解答>
あわてて考えようとすると方針が立たずに、ただひたすら数えることになりそうな問題です。順序を決めて、通る交差点を絞り込んで数えていく方法もありますが、ここでは「道順の問題」と「順列」の関連性を意識しながら解いてみましょう。
まず、AからBまで最短の道のりで進む方法は全部で70通りあります。これは図の中の交差点に数字を書きながら足し算を繰り返すことでもとめることもできますが、順列と組み合わせを使うと、
「右」方向へ4回、「上」方向へ4回進めばBに着くことから、「右・右・右・右・上・上・上・上」という8文字の並べ方が何通りあるかという問題になります。8個の順列から、右4個、上4個のダブり分を除けばよいので、
(8×7×6×5×4×3×2×1)÷(4×3×2×1)÷(4×3×2×1)=70(通り)
この考え方をもとに問題を解いていきます。
(1)3回曲がるということを最も簡単に表すと「右→上→右→上」(右から始める場合)です。AからBに行くにはあと「右」「上」が2個ずつ必要です。
そこで、残りの「右」と「上」をはじめの4個の「右」や「上」のところにつけてやれば、同じ「右→右」なら曲がらないので大丈夫です。
つまり、
| 右 | 上 | 右 | 上 |
この4つの箱を用意して、残りの「右」2個は青い箱、「上」2個は赤い箱に入れる入れ方を数えればよいことになります。
ここで、「右」2個の入れ方は、下の表のように3通りあります。
| 右 | 上 | 右 | 上 |
| 右・右 | × | ||
| 右 | 右 | ||
| × | 右・右 |
「上」2個の入れ方も同様に3通りあるので、全部で 3×3=9(通り) あります。
これは、「上→右→上→右」(上から始める場合)でも同じだけあるので、
3回曲がる方法は、 9×2= 18(通り)
(2)(1)と同じように考えると、4回曲がるのは「右→上→右→上→右」です。
残りは「右」1個、上「2個」です。「上」2個の場合は(1)と同様に3通り、「右」1個については下の表のように3通りです。
| 右 | 上 | 右 | 上 | 右 |
| 右 | × | × | ||
| × | 右 | × | ||
| × | × | 右 |
つまり、 右から始める場合が 3×3=9(通り) なので、
4回曲がる方法は、全部で 9×2= 18(通り)