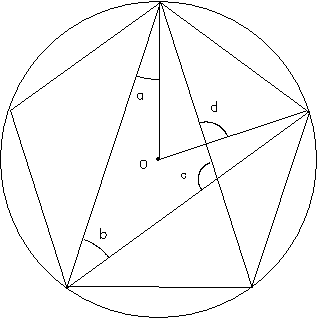
<問題>
下の図のように、点Oを中心とする円周上に正五角形の5個の頂点があります。4個の角度、a,b,c,dの和は【 】度です。

(04年横浜共立A)
入試問題に挑戦第111回解答編
<解答>
三角形の外角を使って解く方法をここでは紹介しましょう。
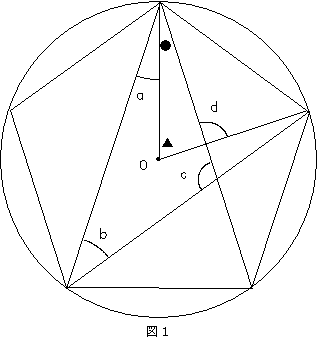
上の図1で ●+▲=d
よってa+b+c+dは、三角形の3つの内角の和と▲との和になります。
▲は360度を5等分する大きさなので、360÷5=72(度)となり,a、b、c、dの和は
、
180+72=252(度)となります。
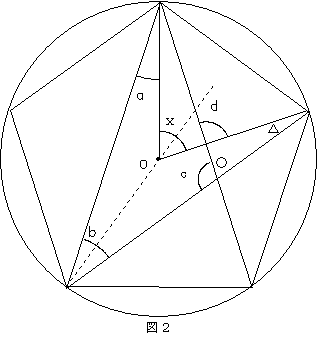
また、図2のように○+△=d
であり、c+○
(180度)とX(72度)との和と考えることもできます。
具体的に必要な角度は、正五角形を分割したときにできる二等辺三角形の頂角の72度と気
付くことができると手際よく処理できます。
図形の見方を問う問題です。(ちなみに、それぞれの角度は、a=18度、b=36度、c=108度、d=90度です。)
実は、まだまだいろいろな考え方ができます。奥の深い、非常に面白い問題です。