<問題>
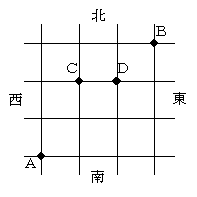
図のように、東西にはしる道が4本、南北にはしる道が4本ある。

(1)A地点からB地点に行く経路のうち最短の経路は【アイ】通りある。
(2)A地点からB地点に行き、続いてC地点に行く経路のうち最短の経路は【ウエ】通りある。ただし、A地点からB地点に行くときにC地点を通ることがあってもよい。
(3)A地点からC地点とD地点の両方を通ってB地点に行く経路のうち最短の経路は【オ】通りある。
(4)A地点からB地点に行く最短の経路のうち、C地点とD地点の少なくとも一つの地点を通るものは【カキ】通りある。
(5)A地点からC地点とD地点の両方を通ってB地点に行き、続いてB地点からC地点もD地点も通らずにA地点にもどる経路のうち、最短の経路は【クケ】通りある。
(04年大学入試センター試験)
入試問題に挑戦第103回解答編
<解答>
今回はセンター試験から小学生でも解くことができる問題を選んでみました。
(1)たし算を利用した最短経路の計算を使って考えてみると、下の図のようになり【20】通り。
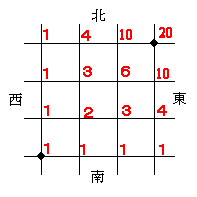
(2)AからBまでは(1)から20通りで、その後BからCへは、下の図から3通り。よって、A→B→Cは20×3=60で、【60】通り。
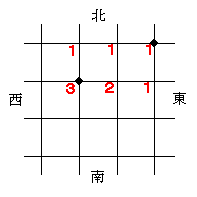
(3)下の図より、AからCまでが3通り、CからDまでが1通り、DからBまでが2通り。
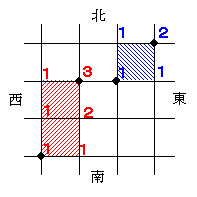
よって、A→C→D→Bは、3×1×2=6で、【6】通り。
(4)全ての通り数から、「CとDの両方を通らない」通り数をひくと、「CとDの少なくとも1つは通る」通り数を求めることができる。
「CとDの両方を通らない」通り数を求めるには、下の図のように、CとDにつながる道を削除してから道順を計算すればよい。
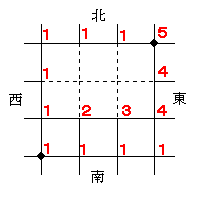
よって、20−5=15で、【15】通り。
(5)行きに(3)、帰りに(4)の答えを利用して計算すると、6×15=90で、【90】通り。