入試問題に挑戦第２回
　ある円の円周を９等分する点を結んで正九角形をつくり、頂点の１つをＡとします。次に、同じ円周を１２等分する点を結んで、１つの頂点がＡに重なるようにして正十二角形を作ります。２つの正多角形の辺で作られる角のうち９０°以下のものは何度ものがありますか。角度をすべて書きなさい。（０１年大阪星光）

入試問題に挑戦第２回・解答編
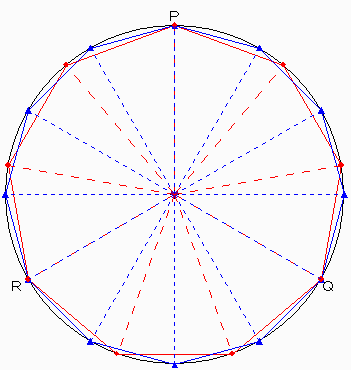
　この問題は図形の特徴をしっかり捉えること、そして自分で作図しながら考えてみることが大切です。まずは下の図を見てください。点Ｐを問題の頂点Ａとすると、そこから正九角形と正十二角形を描くと、それぞれの辺が交錯し、無数の角度が存在します。ここで面倒くさがったり、あきらめたりしてはいけません。もう一度、図をよく見ると、円周の９等分点●と１２等分点▲が、Ｐ・Ｑ・Ｒの３ヶ所で重なっていることがわかります。つまり、円の中心からＰ・Ｑ・Ｒに引いた直線でこの図形を３等分すると、どれも同じものになります。実際に調べるのは、ＰからＱまで、全体の３分の１だけでよいのです。

　さらに、ＰからＱまでの図形に注目すると、下の図のように直線ｌについて線対称な図形なので、調べるのはＰから直線ｌまで、つまり全体の６分の１だけでよいことがわかります。

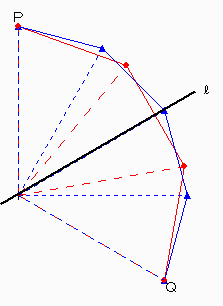
　では、全体の６分の１について、詳しく調べてみることにします。９０度より小さい角度は、下の図のように５ヶ所ありますが、そのうちＣとＥところについては、対頂角になるので、角度の大きさは●・■・▲の３種類しかありません。ここで、Ａにところの●については、正九角形と正十二角形の１つの内角の差の半分なので、

　　（１５０−１４０）÷２＝５度……●

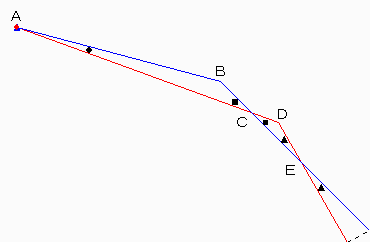
　次に、Ｃのところの■については、下の図のようにＢのところを延長したときにできる角度は、正十二角形の１つの外角なので、３６０÷１２＝３０°。また、この角度は上の図の三角形ＡＢＣについて、Ｂの外角になるので、●＋■＝３０°。これから、

　　３０−５＝２５度……■

　さらに、Ｄのところを延長してできる角度は、正九角形の１つの外角なので、３６０÷９＝４０°。この角度は三角形ＣＤＥについて、Ｄの外角になるので、■＋▲＝４０°。これから、

　４０−２５＝１５度……▲

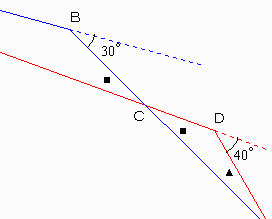
　以上、求める角度は、【　５度、１５度、２５度　】の３つになります。

　このような問題では、いい加減な作図をすると、そこから図形の対称性を見つけだすことが非常に困難になります。精密な作図は不可能ですが、最低限の図形の特徴が確認できるような作図を心掛けたいところです。